/blog/ekd123

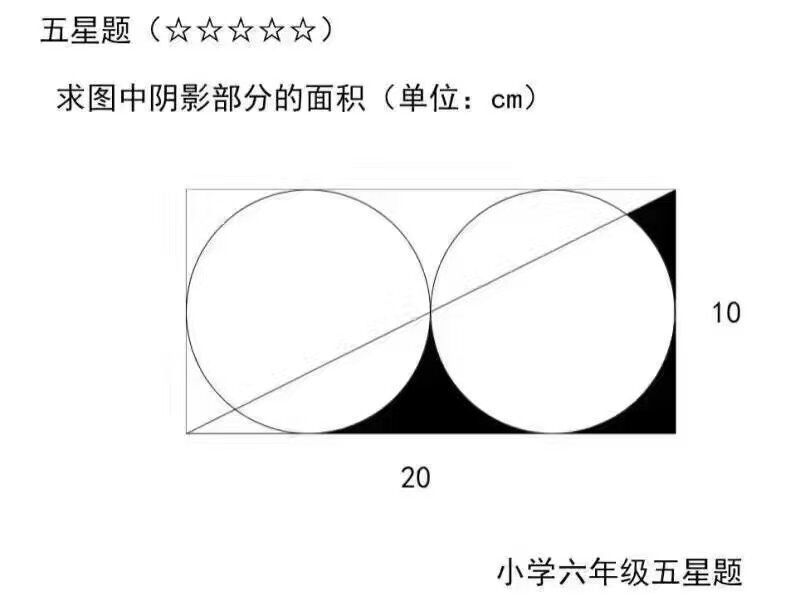
首先评价：这道题肯定不是小学水平，至少是初中奥赛（要用三角函数），不过高中生水平应该会做。如果真是一道小学题，那么左下角那一块要涂满。

根据对称性，很容易看出来，如果填上左下角（下图中的ADE区域），那么阴影部分面积会很好求，矩形面积减去两个圆面积除以 2 就行了（这也正是小学题水平，但肯定算不上什么五星题）。

现在问题转化为求左下角（ADE）的面积。先画几条辅助线。

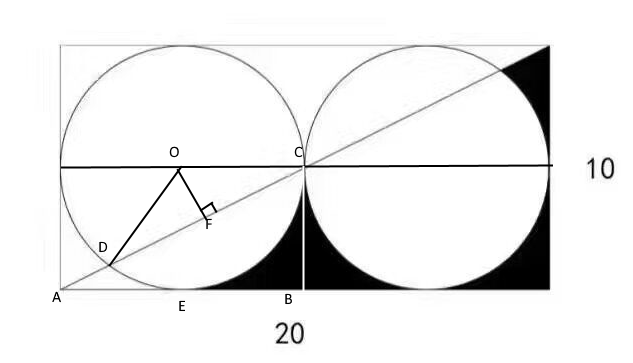
显然有 S_ADE=S_ABC-S_DEBC，略加运算得到 [tex]S_{ADE}=\frac{25\pi}{4}-(S_{ODEC}-S_{ODC})[/tex]。

为了求 S_ODEC 和 S_ODC，有必要知道 ∠DOC。易得 tan∠OCD=tan∠CAB=0.5。为了方便，把 ∠OCD 记作 α，则有 ∠DOC=θ=π-2α。

首先可求出 S_ODEC：[tex]S_{ODEC}=\frac{25\theta}{2}=\frac{25}{2}(\pi-2\arctan\frac{1}{2})[/tex]。

根据几何关系：OF=5sinα，CF=5cosα，则 S_ODC = 12.5sin2α = 10。这里需要一定的三角函数知识才可得解。

现在把这些数据代回 S_ADE 的运算式中即得结果 [tex]10+25\arctan\frac{1}{2}-\frac{25\pi}{4}[/tex]，约等于 1.956。

剩下的事情就很好办了，可以得到最终结果——原图中阴影部分面积 [tex]90-\frac{75\pi}{4}-25\arctan\frac{1}{2}[/tex]，约等于 19.50。

小学题中不可能出现三角函数，所以这不可能是一道小学题，而是有人故意涂掉了区域ADE出来骗人的……有人似乎通过微积分得解，大概挺复杂，懒得用那个方法算了，不过这个几何办法也挺麻烦的。